体素光线投射渲染技术深度探析
体素光线投射渲染详解
正如Pixel(像素)是名词Picture(图片)和Element(元素)的融合,Voxel(体素)其实也是Volume(体积)和Element的融合,因此Voxel其实是指体积元素,和乐高积木或者金字塔的石块在概念上是一样的,构造的对象是一个具有体积的实体,而三角形网面构造出来的对象就像一个空壳或者实体的表面。
在电子游戏中Voxel已经被多次应用,但是它常见的传统应用场合是医学领域,这是因为它能很好地把连续横切面影像(例如 MRI核磁共振成像扫描仪生成的影像)重构为实体。
然而采用Voxel来重现实体并非一个完美的办法,在现实世界中,没有多少东西只由一堆四方块组装而成的,大多数的东西并不能透过Voxel重构来获得准确的实体。在图3中,你看到的就是通过Voxel构建而成的一个非常粗糙的圆环面。

图3 通过Voxel构建而成的圆环面,小方块使得这个图形显得简单而粗糙。
不过类似的问题在大多数游戏中所采用的三角形网面构成的模型中也是存在的,这些模型也是一些近似的构造,只不过你可以使用更多的三角形来获得趋近于真实的模型。Voxel同样可以透过采用更精细的栅格来减轻这个问题。不过这样一来,就会带来更多的内存消耗,这也正是采用Voxel所带来的主要缺点。
举个例子,一个1024 Voxel栅格,将消耗10243×4(RGBA)的内存空间,这相当于4GB的内存(假设RGBA各通道只是8位大小),这样的内存消耗根本谈不上实用,但是幸运的是我们有一个解决方案来减轻这个缺点,它就是octrees或者说octaltrees(八分树)。
“Tree(树)”是在计算机科学中经常采用的数据结构,因为它可以把数据层次化。当你在使用计算机文件的时候,其实所有人每天都无意中在和“树状结构”打交道。
在一个树状结构文件系统中,有硬盘的“根(我们通常使用 “/” 或者“”来表示)目录”,根目录中包含若干个“枝干”(目录),每个枝干包含若干“枝丫”(子目录),周而复此,直到我们看到的“叶片”(文件),只对树结构中的一部分进行存取要比对所有部分都分散分布的结构存取高效得多。树的节点可以有多个分叉,如果多有两个分叉的话,我们就称这样的树结构为二分树(binary tree),如果是0个或者4个分叉的话就是四分树(quaternary tree(quadtree)),如果是0个或者8个分叉的也就自然称作八分树(octree)了。
那么树结构在Voxel渲染上怎么用呢?前面我们提到,Voxel是以规整的栅格方式存放,这样的方式由于连空白位置也都予以编码,存在着巨大的浪费。八分树能透过只在需要之时才动用细密分辨率的办法来提高内存空间的使用效率。为了简化问题,下面我们使用一个二维的空间对此方法进行阐述(图4)。

图4
在这个12×12的栅格中我们画了一个圆形,由于分辨率太低了,因此这个圆实在太粗糙了,不过另一方面,你可以看到栅格中有不少的地方是空白的,这些空间事实上都没有被使用到,但是却仍然被保留起来了。如果使用四分树结构的话,情况就会如图5所示。
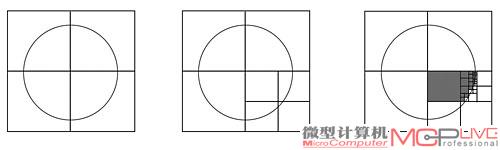
图5
四分树的建立相当简单:打开原图,在各个方向上平分两份,形成四个象限。当一个象限完全位于空白处或者完全被圆形覆盖的话,就停止拆分计算。如果象限只有一部分被覆盖,那么拆分计算就继续进行下去。这样的拆分动作一直进行,直到所有的象限都是同类型(都被覆盖或者都是空白),又或者已经达到了给定的拆分深度(我们在这里的例子是停止于树深4,即每个部分受覆盖的维拆分到 16份)。正如你所看到的那样,即使是采用我们这样简单的拆分深度,获得的终结果也更接近于原始的圆形并且只需要更少的空间存放(97个栅格,而正规的栅格需要122个栅格)。而我们接下来说的八分树,不过是将这个技术扩展成三维(图6)。
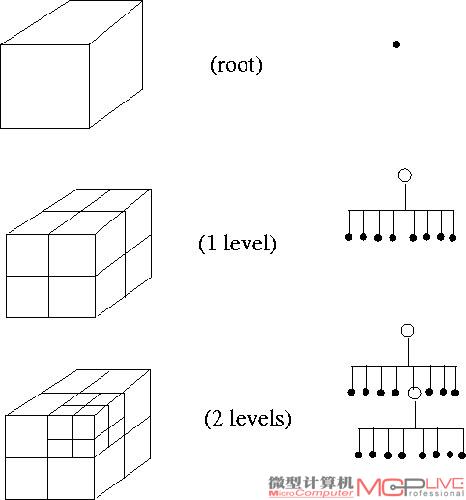
图6 八分树是由四分树技术拓展为立体方式
在实际应用中,按照上面的定义所能增加的内存空间可能要比你想象的少一些。这是因为在一个规整的栅格中,Voxel的位置是固定的。与之相反的是,在八分树中每个节点都必须维持一个连通其子级树的链接,而每个节点本身还必须具备Voxel所需的色彩、法线等8个内存指针。不过和八分树的许多其他优点相比,这只是个小缺点。为了让你能对八分树所具有的更重要贡献有充分的了解,我们必须首先对八分树数据结构如果显示到画面上进行阐述。有多种方式把呈现Voxel,但是id Software选择的方式被称作Ray Casting(光线投射)。






