窥视灵魂深处 AMD新一代SIMD指令集剖析

FMA指令

FMA指令是AVX指令集的一个分支，因此FMA指令使用的是与AVX指令同样的编码设计规则。事实上，Intel的FMA指令集也吸取了AMD提出的SSE5指令集的精髓，FMA指令的fused-multiply-add（融合乘加）与SSE5中的multiply-add/subtract运算如出一辙。当前FMA指令已分为2个版本：

FMA3版本：这是Intel实现的，提供了3个操作数。

FMA4版本：这是AMD实现的，提供了4个操作数。

FMA指令实现了多样的融合乘加/减操作，包括：

fused-multiply-add（融合乘加）操作，例如：VFMADDPS指令等。它做的操作表示为：d = (a * b) + c

fused-multiply-subtract（融合乘减）操作，例如：VFMASUBPS指令等。它做的操作表示为：d = (a * b) - c

fused-multiply-add/subtract interleave（融合乘与交互加减）操作，例如：FMADDSUBPS指令，FMASUBADDPS指令等，操作数必须为vector数据，因此：可以一串式子表示为：d[1] = (a[1] * b[1]) + c[1]，d[0] = (a[0] * b[0]) -c[0]　这意味着vector中的数据交互进行融合乘加/减。

signed-reversed multiply on fused multiply-add（负融合乘加）操作，例如：VFNMADDPS指令，这表示：相乘后取负然后相加，即：d = - (a * b) + c

signed-reversed multiply on fused multiply-subtract（负融合乘减）操作，例如：VFNMSUBPS指令，这表示：相乘后取负然后相减，即：d = - (a * b) - c

这些FMA指令集包括256位的浮点vector运算，还提供了128位的浮点vector数据与scalar数据运算。对浮点运算来说，FMA指令可谓提供了质的效能飞越。

AMD的FMA4版本

AMD在FMA指令上实现了4个operands（操作数），被称为FMA4版本。对于上面第一个例子，我们用FMA4指令可以描述为：

// FMA4 指令

vfmaddsd xmm0, xmm1, xmm2,xmm3（表示xmm0 = xmm1 * xmm2+ xmm3）

vmovsd mmword ptr [d], xmm0（表示d = xmm0）

可以看到AMD的FMA4指令支持4-operand（4个操作数），这样可以无损地使用目标操作数，图1直观地表达了vfmaddsd指令的操作：

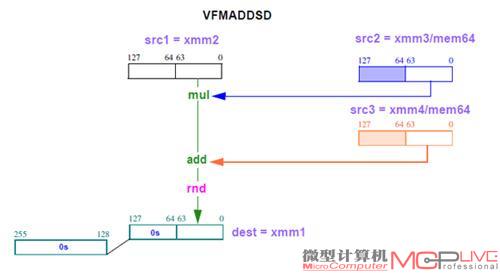
图1

Intel的FMA3版本

在FMA3版本中，其中一个操作数既是源操作数又是目标操作数，上面的示例使用FMA3指令描述如下：

// FMA3 指令

v fma d d213s d xmm1, xmm2,xmm3（表示xmm1=xmm1*xmm2+xmm3）

vmovsd mmword ptr [d], xmm1（表示d=xmm1）

在FMA3版本中第1个源操作数也是目标操作数，vfmadd213sd指令的操作过程如图2所示：

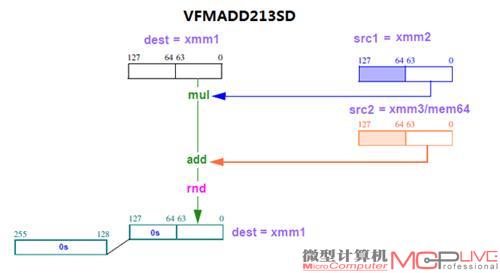
图2 我们看到这个图上表示了src1和dest操作数都是xmm1寄存器。

FMA3与FMA4指令设计的差异

AMD的FMA4指令大部分是从SSE5分离出来，并增加了少量的新指令。FMA3指令与FMA4指令在规格上是一致的，它们相同之处都是进行相同的运算，但是实现方式有些区别。两者除了在操作数上有别外，大的差异在指令的Mnemonic（助记符），由于Intel的FMA3指令是3个操作数，因此额外增加了123的mnemonic方法来表达指令操作数的顺序，数字的意义如下：

1表示：第1个源操作数（也是目标操作数），它由ModRM.reg寻址

2表示：第2个源操作数，它由VEX.vvvv寻址

3表示：第3个源操作数，它由ModRM.r/m 寻址

这些数字的排列顺序有着特殊的意义：

排在第1位表示：被乘数

排在第2位表示：乘数

排在第3位表示：加数或者减数

举个例子：231的mnemonic的排列表示：

第2个源操作数是被乘数

第3个源操作数是乘数

第1个源操作数是加数或减数，目标操作数原来存放的就是加数或减数。

vfmadd231ps ymm0, ymm1, ymmword ptr [mem]
　             -----  ----  -----------------
               加数  被乘数  乘数